Ch 1. Introduction
RL 的目標:學習怎麼在給定狀態下,輸出可以得到最大的獎勵 (reward) 的動作 (action)。
RL 最特別的性質:
- trial-and-error search
- delayed reward
Reinforcement learning 和其他 -ing 結尾的主題類似 (e.g. machine learning),同時是個問題也是解決問題的方法。區分問題和解法在 RL 非常重要,搞不清楚時常會造成困惑。
RL 借用動態系統理論 (dynamical systems theroy) 的馬可夫決策過程 (Markov decision processes) 的觀念來形式化。基本觀念:一個 學習代理 (learning agent) 會隨著 時間 與 環境 (environment) 互動來達成一個 目標 (goal)。學習代理必須可以:
- 感測環境的 狀態 (state)
- 採取 動作 (action) 來影響環境的狀態
馬可夫決策過程以三個觀點提供最簡化的形式涵蓋這個問題:
- sensation
- action
- goal
機器學習三大類:
- supervised learning (監督式學習)
- unsupervised learning (非監督式學習)
- 增強式學習
不同之處:
- RL 與 supervised learning 的不同:(略)
- RL 與 unsupervised learning 的不同:(略)
RL 必須在 exploration (探索) 和 exploitation (利用) 之間取捨:
- 利用:為了要獲得大量的獎勵,RL 代理必須偏好選擇「過去嘗試過最好的」動作
- 探索:為了做到這件事情,必須探索沒有嘗試過的動作
RL 的基本組成:
- the agent (智慧主體,主動進行動作並影響環境狀態的主體)
- the environment (環境)
- RL 系統的子元素:
- a policy (策略)
- a reward signal (獎勵訊號)
- a value function (價值函數)
- (optional) a model of the environment (環境的模型)
策略定義了智慧主體的行為。在給定一個時間點,智慧主體從環境接收狀態,並選擇動作來改變環境。而策略是狀態到動作的映射函數。
- 可能是簡單的函數或是查表,也可能是會涉及複雜計算的演算法
- 可能是隨機性的,提供採取每個動作的機率
獎勵訊號定義了 RL 問題的目標。在每個時間點,環境會傳送單一數值的訊號給 RL 智慧主體,稱為 獎勵。獎勵給學習代理定義事件的好壞。
- 可能是一個隨機性的函數,根據環境的狀態和採取的動作
一個狀態的 價值 是智慧主體預期未來會在這個狀態下取得多少獎勵的總和。
- 以最大的價值而非最大的獎勵來採取動作。
- 獎勵是立即的回饋,價值函數是長期的
- 獎勵是主要的,價值函數是次要的。
- 沒有獎勵就沒有價值,估計價值的唯一目的是獲得更多的獎勵。
- 決定價值比獎勵更難
- 獎勵通常可以直接由環境取得
- 價值必須估計、以及來自一個生命週期觀測的結果來重新估計
模型 用來模擬環境的行為。例如:給定狀態和動作,模型要預測下個狀態和下個獎勵
模型是用來 planning (規劃)
- model-based
- model-free
- trial-and-error
- 極度依賴狀態:作為輸入給策略、價值函數和模型,以及來自模型的輸出。
- 本書探討的問題是假設狀態已經被良好的處理過,可以直接使用。
- 為了專注在討論決策問題,不考慮如何設計狀態的訊號的問題。
- 大部分 RL 的方法都圍繞在如何估計價值函數,但這非 RL 的必要條件。不涉及估計價值函數的方法的例子:
- 基因演算法 (genetic algorithms)
- 基因規劃 (genetic programming)
- 模擬退火法 (simulated annealing)
- 以上是演化式 (evolutionary) 方法,在生命週期中不學習,而是在下個世代產生具備能力的個體。
- 什麼情況下演化式方法會有優勢:
- 如果策略空間很小,或是容易被找到、有足夠多的時間搜尋
- 當無法從環境中感測出完整的狀態
- 本書專注在環境互動中學習的方法,不包含演化式方法。
井字遊戲是個簡單的問題,但沒有辦法由經典的演算法來適當的解決。以下舉幾個例子來說明:
- 使用 minimax
- 使用動態規劃
- 使用演化式方法
- 使用 RL 並配合價值函數
- 這個方法假設了對手的遊戲策略
- 讓玩家無法到達一個「可能會輸掉、但實際上對手可能會失誤而因此勝利」的狀態。
- 需要關於對手的完整規格,包含在每個狀態下會以何種機率採取行動。通常這種資訊是不會先驗的 (a prior) 獲得,大部分實務也不會有。
- 有一種方式是學習模型來模擬對手的行為,再根據模型來計算動態規劃求出最佳解。最後,這個方法和某些 RL 的方法並無不同。
- 直接搜尋所有可能的策略,找出一個有高機率獲勝的方法。
- 此處的策略是一個規則來告訴玩家要下哪一步,對遊戲所有可能狀態 — 每個可能的 O 或 X 的設定 (configuration)
- 對每一個策略,藉由大量的對戰來估計勝率。
- 藉由估計值來決定下一次的策略。
- 可能會用的經典演化式演算法:
- 爬坡演算法 (hill-climbing algorithm),會連續的生成和估計策略
- 基因演算法類
步驟如下:
- 設定數值表 (table of numbers),每一個代表這場遊戲中可能的狀態,每一個數值是當前狀態下勝率的最新估計值。
- 把這個估計值當作這個狀態的價值,整個表就是學習到的價值函數。
- 對於所有三個連一直線的狀態的勝率是 1 (或是 0,被對手成功連線時) 。
- 所有其他狀態的勝率值都初始化為 0.5。
- 接下來開始對戰很多次。
- 選擇要下的點,大部分情況下可以使用貪心法挑選最大的價值,也就是最高的勝率。
- 少部份的情況下選擇其他沒有下過的落點,這稱之為 探索,讓我們可以看過沒見過的狀態。
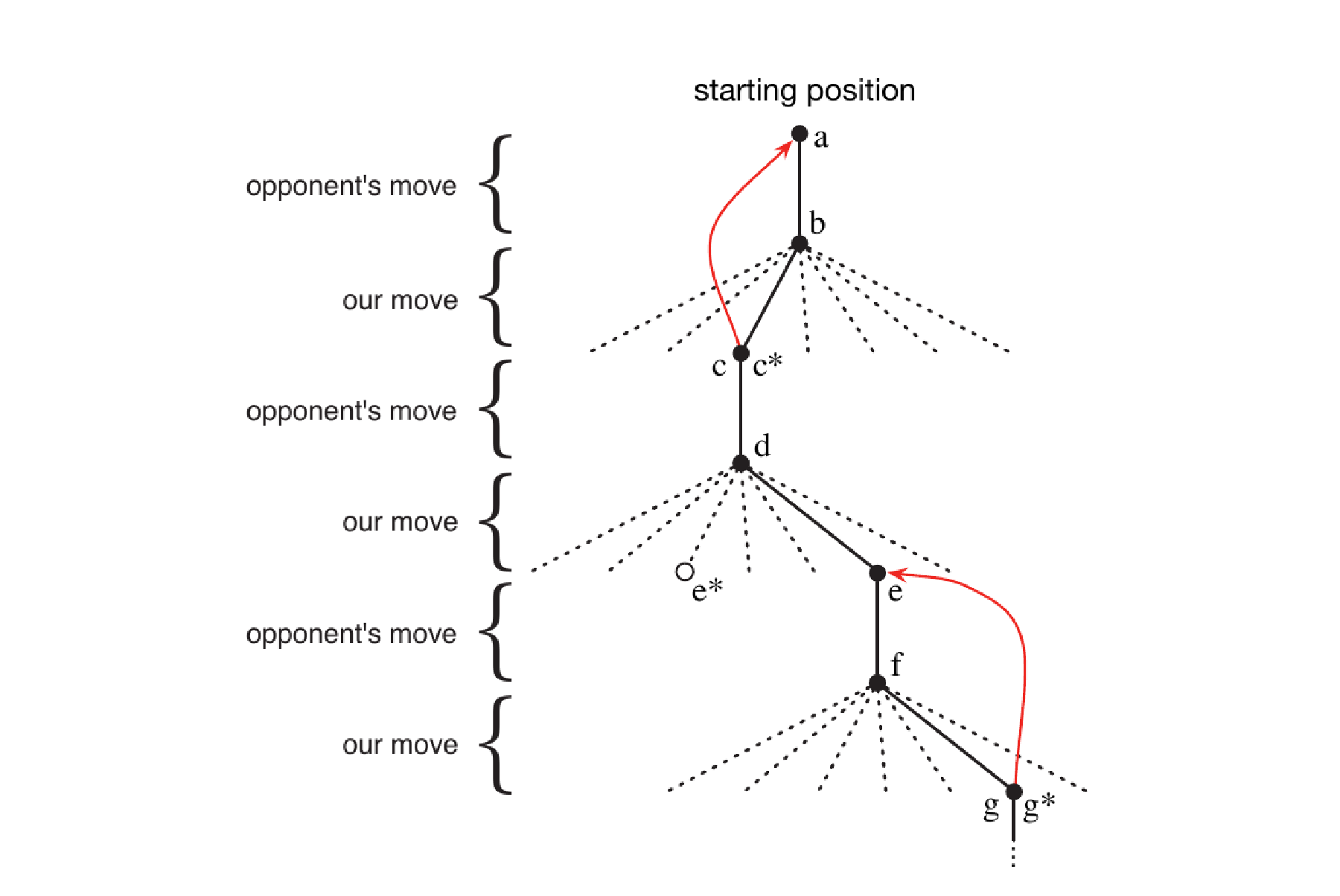
- 在遊戲過程中會更新價值函數,使估計的更準確。方式是在每一步過後回補 (back up) 前一步的狀態的價值。
- 假設當前狀態是 $S_{t}$,經過一個貪心選擇過後下一步是 $S_{t+1}$,這時會更新 $S_{t}$ 的價值函數,標記為 $V(S_{t})$。可以被列式如下:
- $V(S_{t}) \leftarrow V(S_{t}) + \alpha [ V(S_{t+1}) - V(S_{t})]$
- $\alpha$: 步長參數 (step-size parameter)
- 這是一個 temporal-difference 學習法的例子
- $V(S_{t}) \leftarrow V(S_{t}) + \alpha [ V(S_{t+1}) - V(S_{t})]$
這個方法在這個任務上可以做得很好,因為:
- 步長參數在經過一段時間後適當的減少,會收斂到在給定每個狀態下真實的勝率值。
- 每一步都是根據對手的落子下的最佳解。
這個例子突顯了 RL 的關鍵特色:
- 強調在與環境互動中學習
- 目標明確
- 不只根據當前的狀態,也會考慮後面的發展